DOĞADA ALTIN ORAN

Bitkilerde Altın Oran:
Bitkilerde dallanma aralıkları ve yaprakların dizilişi güneş ışığından en fazla ve en verimli alacağı şekilde oluşur. Bu biçimdeki dizilişte, biri ötekinin güneş ışını almasına en az engel olur. Bu olgu, bitkinin sağlıklı büyümesi için gereklidir. Botanikçiler, bitkilerdeki bu dallanma olgusuna “phyllotaxis” ve Y/P = (dallanma periyodu /yaprak sayısı) oranına yaprak ıraksaması derler. Yaprak ıraksaması, ardışık Fibonacci sayılarının oranıdır.[1]
Şekil 2’de bitkinin yaprakları yandan ve üstten görünmektedir. Yaprakların birbirlerini gölgelemeyecek biçimde sıralanmış olduklarına dikkat ediniz. Çevremizde gördüğümüz ağaç ve çiçeklerin yaprakları bize ilk bakışta rastgele dizilmiş gibi görünebilirler, ama onları biraz ayrıntılı incelediğimizde şaşırtıcı birer geometrik yapıya sahip olduklarını görebiliriz. Bu geometrik yapı onlara en iyi büyüme ve gelişme koşullarını yaratmaktadır.
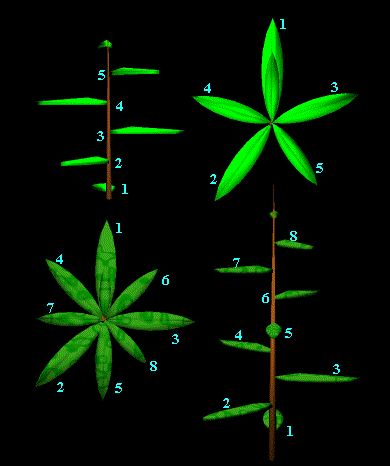
Şekil 3a’daki bitkinin dal sayılarını dikkatle inceleyiniz. Sırasıyla, bölmelerdeki dal sayıları 1, 2, 3, 5, 8, 13’tür. Bunların Fibonacci dizisinin öğeleri olduğunu biliyoruz.
Şekil 3b’de aynı bitkinin yaprak sayılarına bakınız. Her bölmedeki yaprak sayıları, sırasıyla; 1, 2, 3, 5, 8, 13 Fibonacci sayılarıdır. Bu oluşumu pek çok bitkide görebiliriz. Bu sıralanış, bitkilerdeki düzen ve estetiğin tamamıyla matematiksel kurallara dayandığını göstermektedir.
Çiçeklerin taç yapraklarının ve tohumlarının sayısı genellikle Fibonacci sayı dizisindeki 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… ardışık sayıları olur. Elbette bu kurala uymayan bitkiler de vardır. Çünkü doğada altın oran haricinde başka geometrik veya matematiksel sistemler de vardır.
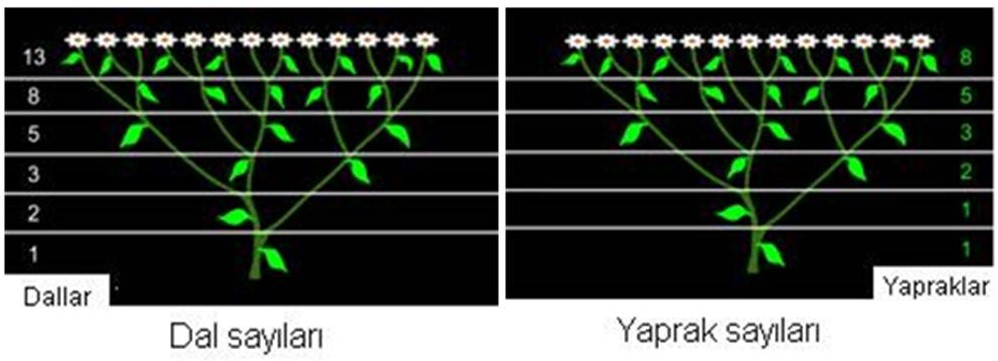
şekil 3a şekil 3b
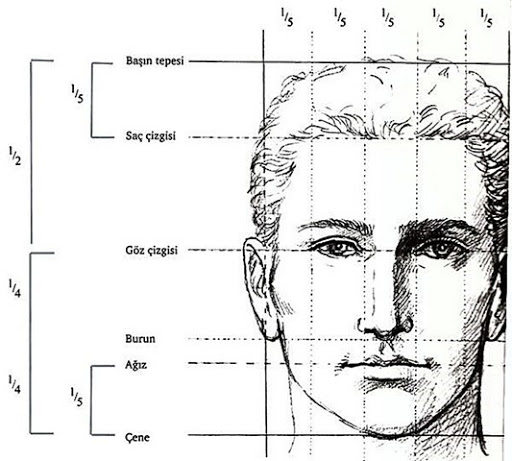
Doğada Fibonacci sayılarının ve altın oranın nasıl kullanıldığını sayısız örnekte görebiliriz. Leonardo da Vinci ve Corbusiergibi tanınmış pek çok sanatçı, bilim adamı ve tasarımcılar; inceleme yaparken ya da eserlerini yaparken hep altın orana göre belirlenmiş insan bedenini esas almışlardır. Günümüz mimarlarının en önemli başvuru kitapların1dan biri olan Neufert’te de altın orana göre belirlenmiş insan vücudu esas alınmaktadır.
İnsan Vücudunda Altın Oran:
- Baştan ayak ucuna olan mesafe ile göbek deliğinden ayak ucuna olan mesafe arasındaki oran:1,618
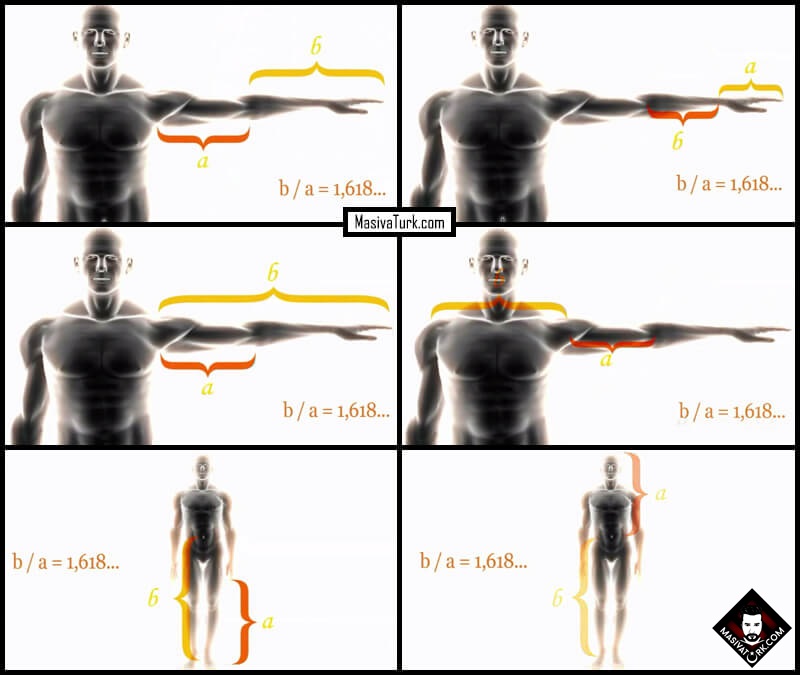
- Omuzdan parmak ucuna olan mesafe ile dirsekten parmak ucuna olan mesafe arasındaki oran:1,618
- Yüz uzunluğu ile çene ucundan kaşların birleşim yerine olan uzunluğun birbirine oranı:1.618
- Ağız boyunun burun genişliğine oranı:1,618
- Burun genişliğinin burun delikleri arasındaki genişliğe oranı:1.618
- Gözbebekleri arasındaki mesafenin kaşlar arasındaki mesafeye oranı:1,618
- Orta parmağın serçe parmağına oranı:1,618
- İşaret parmağımızdaki her boğumun bir önceki boğuma oranı:1,618
İdeal ölçülerdeki bir insan vücudunda altın oranın sağladığı estetiğin dışında farklı geometrik ölçü düzenleri de bulunmaktadır. (Şekil 1)

Şekil 1: İnsan vücudunda altın oranın sağladığı estetiğin dışında farklı geometrik ölçü düzenleri de vardır.
Mikro Dünyada Altın Oran
Geometrik şekiller sadece üçgen, kare veya beşgen, altıgen ile sınırlı değildir. Bu saydığımız şekiller değişik biçimlerde de bir araya gelerek yeni üç boyutlu geometrik şekiller oluşturabilirler. Bu konuda ilk olarak küp ve piramit örnek olarak verilebilir. Ancak bunların dışında, günlük hayatta hiç karşılaşmadığımız hatta ismini dahi ilk defa duyduğumuz tetrahedron (düzgün dört yüzlü), oktahedron,
dodekahedron ve ikosahedron gibi üç boyutlu şekiller de vardır. Dodekahadron 13 tane beşgenden, ikosahedron ise 20 adet üçgenden oluşur. Bilim adamları bu şekillerin matematiksel olarak birbirine dönüşebileceğini ve bu dönüşümün altın orana bağlı oranlarla gerçekleştiğini bulmuşlardır.
Mikro organizmalarda altın oran barındıran üç boyutlu formlar oldukça yaygındır. Birçok virüs ikosahedron yapısında bir biçime sahiptir. Bunların en ünlüsü Adeno virüsüdür. Adeno virüsünün protein kılıfı, 252 adet protein alt biriminin düzenli bir biçimde dizilmesi ile oluşur. İkosahedronun köşelerinde yer alan 12 alt birim ise beşgen prizmalar biçimindedir. Bu köşelerden diken benzeri yapılar uzanır. (Şekil 6a)
Virüslerin altın oranları bünyesinde barındıran formlarda olduğunu tespit eden ilk kişi 1950’li yıllarda Londra’daki Birkbeck Koleji’nden A. Klug ile D. Caspar’dır. Üzerinde ilk tespit yapılan virüs ise Polyo virüsüdür. Rhino 14 virüsü de Polyo virüsü ile aynı formu gösterir.

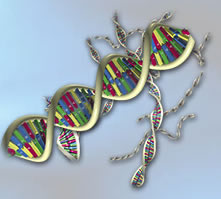
DNA’da Altın Oran
Canlıların tüm fiziksel özelliklerinin kodlandığı molekül yapı DNA da altın orana dayanan geometrik bir şekildedir. DNA düşey doğrultuda iç içe açılmış iki sarmaldan oluşur. (Şekil 7) Bu sarmallarda her birinin bütün yuvarlağı içindeki uzunluk 34 angström genişliği 21 angström’dür. (1 angström; santimetrenin yüz milyonda biridir) 21 ve 34 art arda gelen iki Fibonacci sayısıdır. Ayrıca atomlardaki elektronların sayısının nötronların sayısına oranı da 1,618’dir.

Kar Kristallerinde Altın Oran
Altın oran kristal yapılarda da kendini gösterir. Bunların çoğu gözümüzle göremeyeceğimiz kadar küçük yapıların içindedir. Ancak kar kristali üzerindeki altın oranı gözlerinizle göre bilirsiniz. Altıgen şeklindeki kar kristalini oluşturan kısalı uzunlu dallanmalarda, çeşitli uzantıların oranı hep altın oranı verir. (Şekil 8)

Altın Oran Sarmalları:
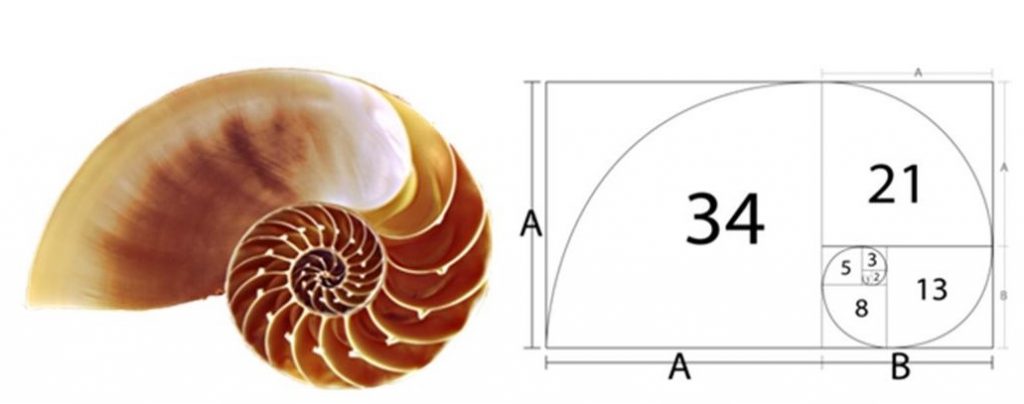
Yumuşakçaların pek çoğunun sahip olduğu kabuk, logaritmik spiral şeklinde büyür ve bu biçimsel yapı yumuşakçalara özel bir konfor sağlarken aynı zamanda sağlam yapılarıyla güvenli bir sığınak da oluşturur. Biyologlar, bu tarz büyümeyi “Gnom tarzı büyüme” olarak adlandırmıştır. Birkaç santimetre çapındaki bir Nautilus yumuşakçasında, gnom tarzı büyümenin en güzel örneğini görmek mümkündür. (Şekil 5) Nautilus’un kabuğunun içinde, sedef duvarlar ile örülmüş bir sürü odacığın oluşturduğu içsel bir sarmal uzanır. Nautilus, büyüdükçe, sarmal kabuğunun ağız kısmında, bir öncekinden daha büyük bir odacık inşa eder ve arkasındaki kapıyı bir sedef tabakası ile örterek daha geniş olan bu yeni bölüme ilerler ve böylece bir sarmal oluşturur.

Şimdi bu sarmalın oluşumunda altın oranın nasıl kullanıldığını inceleyelim. Kenarlarının oranı altın orana eşit olan bir dikdörtgene “altın dikdörtgen” denir. Uzun kenarı 1,618 birim kısa kenarı 1 birim olan veya kenarları ardışık Fibonacci sayıları olan bir dikdörtgen altın dikdörtgendir. Bu dikdörtgenin kısa kenarının tamamını kenar kabul eden bir kare ve hemen ardından karenin iki köşesi arasında bir çeyrek çember çizelim. Kare çizildikten sonra yanda kalan küçük bir kare ve çeyrek çember çizip bunu asıl dikdörtgenin içinde kalan tüm dikdörtgenler için yapalım. Bunu yaptığınızda karşınıza bir sarmal çıkacaktır. (Şekil 5)
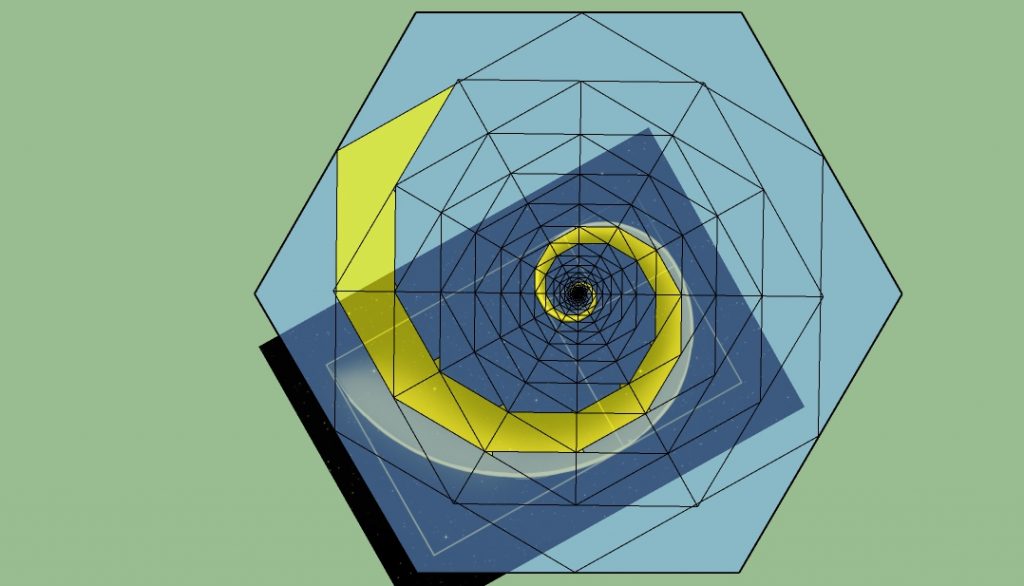
Altın oran sarmalı bir başka yöntemle de üç boyutlu elde edilebilir. Bunun için birbirini saran altıgen fraktaller çizilir. Altıgen kuşakları arasında oluşan üçgenler, 1,73 oranında büyüyerek altın oran sarmalını oluşturur. (şekil 6) Böylece sarmal üç boyutlu olarak çizilmiş olur. Bu sarmal Arap alfabesinde “vav” harfinin ideal hüsnü hat çizimidir ve çok ilginçtir ki “vav” harfinin ebced hesabındaki sayısal değeri de altıdır ve tasavvuf kültüründe “vav” harfi, kainatı yani kosmosu temsil eder. Üstelik Latin alfabesinde kullanılan “6” rakamının biçimsel özelliğiyle de aynıdır. Ezoterik öğretilerde 6 sayısı maddî alemi, 9 sayısı da manevî alemi temsil eder. Bu iki sayının evliliği Çin felsefesindeki yin-yang benzeri “69” sayısal şeklini ortaya çıkartır. Bu da madde-ruh, yer-gök evliliğini ve evrensel düzeni temsil eder.
[1] Mehmet Suat Bergil, Doğada/Bilimde/Sanatta, Altın Oran, Arkeoloji ve Sanat Yayınları, 2.Basım, 1993, s. 77. S.155

Bir cevap
Tşk