FRAKTAL GEOMETRİ
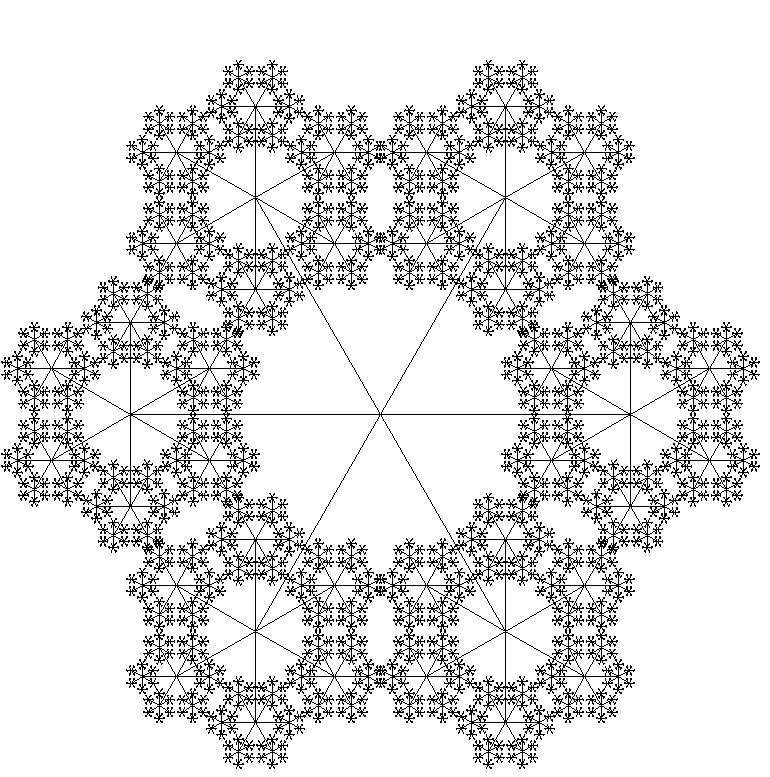
Geometri’de 20. yüzyıla dek Öklid geometrisi kullanıldı; doğrular, düzlemler, üçgenler… Ancak zamanla doğayı daha iyi anlamak ve modellemek için yeni bir geometriye gereksinim duyuldu. İşte bu da fraktal geometriydi. Çünkü doğadaki kutsal geometri fraktaller halinde kendisini gösterir. Fraktal; genellikle birbirine benzeyen değişik geometrik şekillerin genel adıdır. Sonsuza dek iç içe geçmiş ve birbirini tekrarlayan şekillerdir. Bu tanıma göre fraktal ana şekle benzeyen gitgide küçülen alanı sonsuz olan bir şekildir. Fraktalleri ikiye ayırabiliriz :
1- Kendinin tıpatıp aynısı olan fraktaller:
Bu tip fraktallerin herhangi bir parçasıyla, büyük olan parça tıpatıp aynıdır.
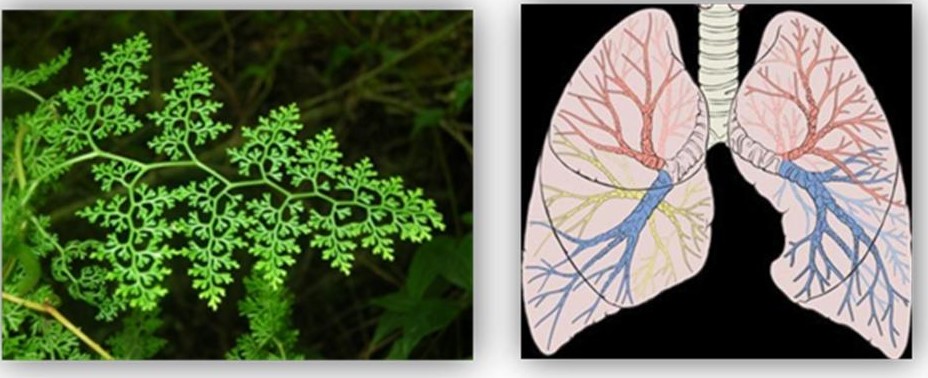
a-Yaprak Fraktali :
Şekilde görülen en küçük yaprak en büyük yaprak nasıl inşa edildiyse o şekilde inşa edilmiştir. (Şekil 9)
b-Akciğer Fraktali:
Akciğerlerimiz fraktale çok iyi birer örnektirler. Dikkat edin soluk borusu ikiye ayrılıyor, sonra tekrar ayrılan damarlar ikiye ayrılıyor, hep ikiye ayrılarak ve daha da küçülerek devam ediyor. Bu da akciğerlerin fazla hava almasını sağlıyor. (Şekil 10)
c-Ağaç Dalı Fraktali:
Aynı Akciğer fraktali mantığı ile oluşturulan Ağaç Fraktali: Kökten başlayarak her zaman ikiye ayrılarak ve küçülerek devam eder.
d-Sierpinski Üçgen Fraktali:
Polonyalı matematikçi Waclaw Sierpinski’nin adını taşır. Eşkenar üçgenin içinden küçük üçgenler çıkartılarak elde edilir. Bu işlemi tekrarlamaya devam edersek Sierpinski üçgenini elde ederiz. (Şekil 11)

2- Kısmen benzer / parçaları – bölümleri fraktal olan şekiller: Bu tip fraktallerin belirli parçaları fraktaldir. Komple, büyük şekle kısmen, parça parça benzerlik gösterir.
a-Koch Kar Tanesi Fraktali
Aşağıda Koch kar tanesi fraktalinin adımlarını inceleyiniz. Bu fraktalin diğerlerinden farkı, kısmen parçalı fraktal oluşudur. 1904 yılında Alman matematikçi Helge Van Koch tarafından açıklanan bu ilginç şekli elde etmek için bir eşkenar üçgen alınır, her kenarı üç eşit aralıkla işaretlenir ve ortadaki bölümler çıkartılır ve bu buralara kenarları çıkartılan parçalar kadar olan yeni eşkenar üçgenler konulur. Bu durumda yeni şeklimizin çevre uzunluğu öncekinin 4/3 katı olmuştur. (Şekil 12)
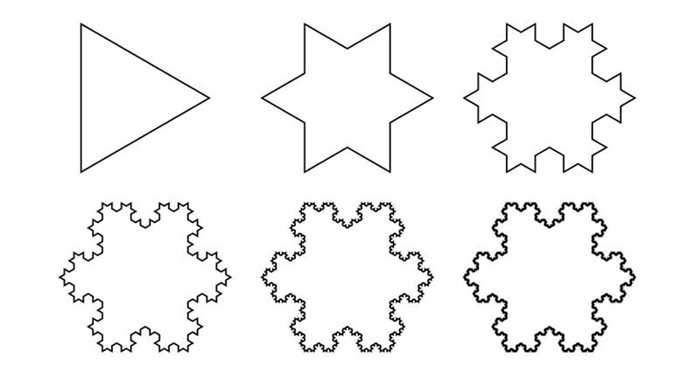
Bu şekilde her yeni adımda, bir önceki adımda elde edilen doğru parçalarına aynı işlem uygulanınca sonuçta fraktal bir şekil ortaya çıkar. İşleme bu şekilde devam edilip n. adıma gelinirse eğrinin toplam uzunluğu (4/3) n olacaktır. Eğer n yeterince büyük alınırsa eğrinin uzunluğu da sonsuza gidecektir. Diğer bir deyişle Koch eğrisinde iki nokta arasındaki uzaklık sonsuzdur. Eğer bu eğri yakından incelenirse şeklin tamamı ile onu oluşturan alt parçaların bir birine benzer olduğu görülür. Örneğin şeklin tamamını 3 kat küçültürseniz bir alt parçasını elde edersiniz. Bu küçültme işlemine sonsuza kadar devam edebilirsiniz.
Koch kar taneciği düzenli denilen, yani çizim kuralları belli olan fraktallere bir örnektir. Bu düzenli fraktallerin ortak özellikleri, eğrinin bir bölümünü ne kadar büyütürseniz büyütün eğri tam olarak aynı şekli sürdürmeye devam etmektedir.
Koch eğrisinin ilginç bir özelliği alanının sonlu olmasıdır, çünkü onu bir daire içine sığdırmak mümkündür. Bununla birlikte her adımda uzunluğu biraz daha artar. Yani alanı sonlu ama çevresi sonsuzdur!

Düz bir alüminyum folyo 2 boyutludur ancak onu buruşturursanız iki artı bir şey boyutunda bir fraktale dönüştürürsünüz. Bu yeni boyutun kesin değeri folyonun ne kadar kırışık olduğuna bağlıdır ve fraktal kar taneciği için kullanılan yöntemle yaklaşık olarak hesaplayabiliriz. Aradaki tek fark, cetvelle uzunluk ölçmek yerine bu sefer sürekli küçülen ölçü plakaları ile alan ölçüyor olmamızdır.
Fraktaller konusundaki çalışmalar bilimin birçok dalında yararlı fikirlere de kaynaklık yapmaktadır çünkü bu geometri doğal olayların matematiksel olarak modellenmesinde avantajlıdır. Yine de bütün bu girişimler yalnızca bir başlangıçtır çünkü fraktallerin boyutsal ayrıcalıkları dışında temel özellikleri henüz tam olarak kavranmış değildir. Mandelbrot’un çalışmasının açtığı bu yeni kapının ardında keşfedilmeyi bekleyen daha nice şey bulunuyor anlaşılan…[1]
Doğada Fraktal Örnekleri:
Fraktal geometrik formlar doğada pek çok canlıda ve varlıkta kendisini göstermektedir: Kırmızı lahanada, eğrelti otunda, piramit karnabaharında, aloe bitkisinde, mercan poliplerinde, deniz kabuklularında, ağaç dallanmasında, yaprak yapısında, buz kristallerinde, kar tanesi kristallerinde, bizmut kristallerinde, kan damarlarında, nöronlarda… (Şekil 13)


[1] Sibel Çağlar, Doğanın Geometrisi – Fraktal Geometri
